Glocke
Inhaltsverzeichnis
\(\\\)
Aufgabe 1 – Fußpunkt F

\(\\\)
Fällen wir das Lot von der Glocke \(G\) auf die Gerade \(g\), so erhalten wir den Lotfußpunkt \(F\). Dieser ist der Punkt der Geraden \(g\), der am nächsten gelegen ist zu der Glocke \(G\). Daraus folgt, dass der Vektor \(\vec{GF}\) orthogonal zu der Geraden \(g\) verläuft und damit auch, dass der Vektor \(\vec{GF}\) orthogonal zu dem Richtungsvektor \(\vec{TU}\) der Geraden \(g\) ist. Wir verwenden diese Eigenschaft, um \(F\) zu bestimmen.
Es gilt
\( \quad \begin{array}{ r c l l } \vec{GF} \circ \vec{TU} & = & 0 \\[6pt] \left(\vec{f} - \vec{g} \right) \circ \left(\vec{u} - \vec{t} \right) & = & 0 \\ \end{array} \)
\(\\\)
\(\vec{f}\) ist zunächst noch unbekannt. Jedoch wissen wir, dass \(F\) ein Punkt der Geraden \(g\) ist. Das heißt, dass mit einem geeigneten \(r\) gilt
\( \quad \begin{array}{ c c l c l } \vec{f} & = & \begin{smallmatrix} \left( \begin{array}{c} 2 \\ 3 \\ 4{,}5 \end{array} \right) \end{smallmatrix} +r \cdot \begin{smallmatrix} \left( \begin{array}{r} -2 \\ 2 \\ 0 \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{c} 2 - 2r \\ 3 + 2r \\ 4{,}5 \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\\)
Wir bestimmen nun \(r\) indem wir alle Vektoren in die Gleichung mit dem Skalarprodukt einsetzen.
\( \quad \begin{array}{ r c l l } \left[ \begin{smallmatrix} \left( \begin{array}{c} 2 - 2r \\ 3 + 2r \\ 4{,}5 \end{array} \right) \end{smallmatrix}- \begin{smallmatrix} \left( \begin{array}{c} 3 \\ 3{,}5 \\ 4{,}5 \end{array} \right) \end{smallmatrix} \right] \circ \left[ \begin{smallmatrix} \left( \begin{array}{c} 0 \\ 5 \\ 4{,}5 \end{array} \right) \end{smallmatrix} -\begin{smallmatrix} \left( \begin{array}{c} 2 \\ 3 \\ 4{,}5 \end{array} \right) \end{smallmatrix} \right] & = & 0 \\[10pt] \begin{smallmatrix} \left( \begin{array}{c} -1 - 2r \\ -0{,}5 + 2r \\ 0 \end{array} \right) \end{smallmatrix} \circ \begin{smallmatrix} \left( \begin{array}{r} -2 \\ 2 \\ 0 \end{array} \right) \end{smallmatrix} & = & 0 \\[10pt] (-1 - 2r) \cdot (-2) + (-0{,}5 + 2r) \cdot 2 + 0 \cdot 0 & = & 0 & \\[6pt] 2 + 4r - 1 + 4r & = & 0 & \\[8pt] 8r & = & - 1 & | : 8 \\[8pt] r & = & - \frac{1}{8} \\ \end{array} \)
\(\\\)
Das \(r\) wird nun zur Berechnung von \(\vec{f}\) eingesetzt.
\( \quad \begin{array}{ c c l c l } \vec{f} & = & \begin{smallmatrix} \left( \begin{array}{c} 2 \\ 3 \\ 4{,}5 \end{array} \right) \end{smallmatrix} -\dfrac{1}{8} \cdot \begin{smallmatrix} \left( \begin{array}{r} -2 \\ 2 \\ 0 \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{c} 2{,}25 \\ 2{,}75 \\ 4{,}5 \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\\)
Damit erhalten wir den Fußpunkt \(F(2{,}25 | 2{,}75 | 4{,}5 )\).
\(\\[2em]\)
Aufgabe 2 – nicht identisch
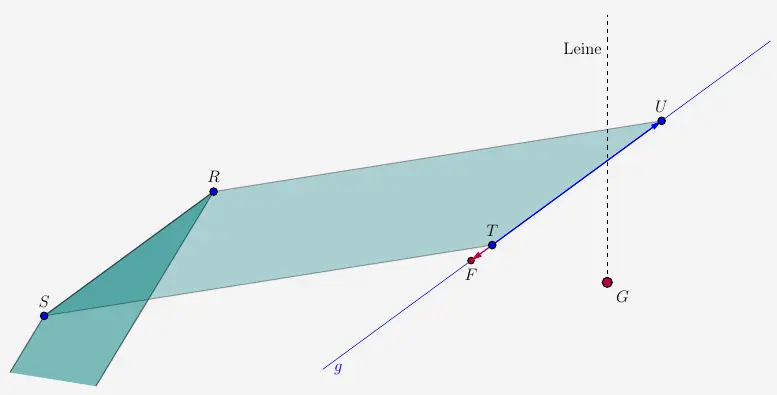
Das negative Vorzeichen bei \(r\) besagt, dass der Vektor \(\vec{TF}\) in Gegenrichtung zu dem Vektor \(\vec{TU}\) verläuft.
\(\\\)
Das bedeutet, dass Punkt \(F\) im Gegensatz zu der ursprünglichen Annahme und Skizze außerhalb des Vierecks \(RSTU\) liegt. Der nächste Punkt \(K\) zu der Glocke \(G\) ist identisch mit dem Eckpunkt \(T\) des Vierecks \(RSTU\).
\(\\[2em]\)
Aufgabe 3 – neue Position
Wir berechnen zunächst den Ortsvektor von \(M\) mit
\( \quad \begin{array}{ c c l c l c l } \vec{m} & = & \vec{t} + \frac{1}{2} \cdot \vec{TU} & = & \begin{smallmatrix} \left( \begin{array}{c} 2 \\ 3 \\ 4{,}5 \end{array} \right) \end{smallmatrix} +\frac{1}{2} \cdot \begin{smallmatrix} \left( \begin{array}{r} -2 \\ 2 \\ 0 \end{array} \right) \end{smallmatrix} & = & \begin{smallmatrix} \left( \begin{array}{c} 1 \\ 4\\ 4{,}5 \end{array} \right) \end{smallmatrix} \\ \end{array} \)
\(\\\)
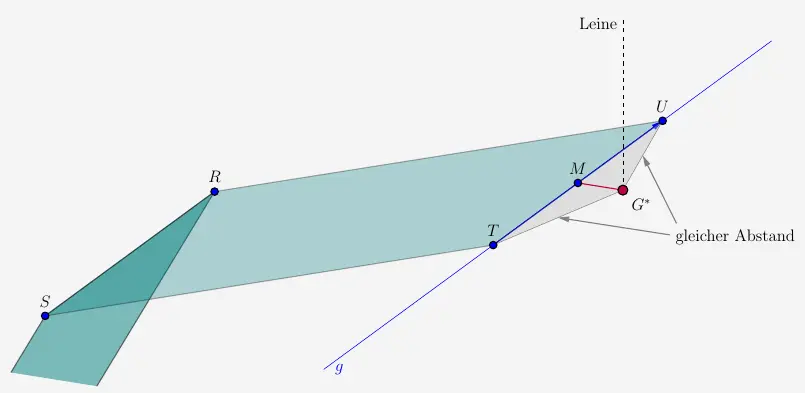
Ist Punkt \(G^*\) gleich weit von \(T\) und \(U\) entfernt, so muss der Vektor \(\vec{MG^*}\) orthogonal zum Vektor \(\vec{TU}\) sein.
\(\\\)
Für die neue Position der Glocke gelten nun folgende Bedingungen:
\( \quad \begin{array}{ r l l l } \textrm{I} & x_3=4{,}5 \\[6pt] \textrm{II} & \vec{MG^*} \circ \vec{TU} = 0 \\[6pt] \textrm{III} & \begin{vmatrix}\vec{MG^*}\end{vmatrix} = 0{,}35 \\ \end{array} \)
\(\\\)
Mit Bedingung \(\textrm{II}\) gilt
\( \quad \begin{array}{ r c l l } \vec{MG^*} \circ \vec{TU} & = & 0 \\[6pt] \left(\vec{g^*} - \vec{m} \right) \circ \left(\vec{u} - \vec{t} \right) & = & 0 \\[8pt] \left[ \begin{smallmatrix} \left( \begin{array}{c} x_1 \\ x_2 \\ 4{,}5 \end{array} \right) \end{smallmatrix} -\begin{smallmatrix} \left( \begin{array}{c} 1 \\ 4 \\ 4{,}5 \end{array} \right) \end{smallmatrix} \right] \circ \left[ \begin{smallmatrix} \left( \begin{array}{c} 0 \\ 5 \\ 4{,}5 \end{array} \right) \end{smallmatrix} -\begin{smallmatrix} \left( \begin{array}{c} 2 \\ 3 \\ 4{,}5 \end{array} \right) \end{smallmatrix} \right] & = & 0 \\[10pt] \begin{smallmatrix} \left( \begin{array}{c} x_1 - 1 \\ x_2 - 4 \\ 0 \end{array} \right) \end{smallmatrix} \circ \begin{smallmatrix} \left( \begin{array}{r} -2 \\ 2 \\ 0 \end{array} \right) \end{smallmatrix} & = & 0 \\[10pt] (x_1 - 1) \cdot (-2) + (x_2 - 4) \cdot 2 & = & 0 & \\[6pt] -2x_1 + 2 + 2x_2 - 8 & = & 0 & \\[6pt] -2x_1 + 2x_2 - 6 & = & - 1 & | + 6 \\[6pt] -2x_1 + 2x_2 & = & 6 & | + 2x_1 \\[6pt] 2x_2 & = & 6 + 2x_1 & | : 2 \\[6pt] x_2 & = & 3 + x_1 \\ \end{array} \)
\(\\\)
Weiter lösen wir die Gleichung \(\textrm{III}\) indem wir \(x_2\) dort einsetzen.
\( \quad \begin{array}{ r c l } \begin{vmatrix} \begin{smallmatrix} \left( \begin{array}{c} x_1 \\ 3 + x_1 \\ 4{,}5 \end{array} \right) \end{smallmatrix} -\begin{smallmatrix} \left( \begin{array}{c} 1 \\ 4 \\ 4{,}5 \end{array} \right) \end{smallmatrix} \end{vmatrix} & = & 0{,}35 \\[10pt] \begin{vmatrix} \begin{smallmatrix} \left( \begin{array}{c} x_1 - 1 \\ x_1 - 1 \\ 0 \end{array} \right) \end{smallmatrix} \end{vmatrix} & = & 0{,}35 \\[10pt] \sqrt{\left(x_1 - 1\right)^2 + \left(x_1 - 1\right)^2 + 0^2} & = & 0{,}35 & | ( \dots )^2 \\[6pt] \left(x_1 - 1\right)^2 + \left(x_1 - 1\right)^2 & = & 0{,}35^2 \\[6pt] 2 \cdot \left(x_1 - 1\right)^2 & = & 0{,}1225 & | : 2 \\[6pt] \left(x_1 - 1\right)^2 & = & 0{,}06125 & | \sqrt{\dots} \\[6pt] x_1 - 1 & = & \pm 0{,}2475 & | + 1 \\[6pt] x_1 & = & 1 \pm 0{,}2475 \\[6pt] x_{1_1} & = & 1{,}2475 & \Rightarrow \quad x_{2_1} \; = \; 4{,}2475 \\[6pt] x_{1_2} & = & 0{,}7525 & \Rightarrow \quad x_{2_2} \; = \; 3{,}7525 \\ \end{array} \)
\(\\\)
Wir erhalten 2 mögliche Positionen von \(G^*\), die sich auf der gleichen Höhe wie Punkt \(M\) befinden:
\( \quad G_1^*(1{,}2475 | 4{,}2475 | 4{,}5) \quad \text{und} \quad G_2^*(0{,}7525 | 3{,}7525 | 4{,}5) \)
\(\\\)
Wir wählen die weiter rechts gelegene Position mit \(G^*(1{,}2475 | 4{,}2475 | 4{,}5)\).
\(\\\)